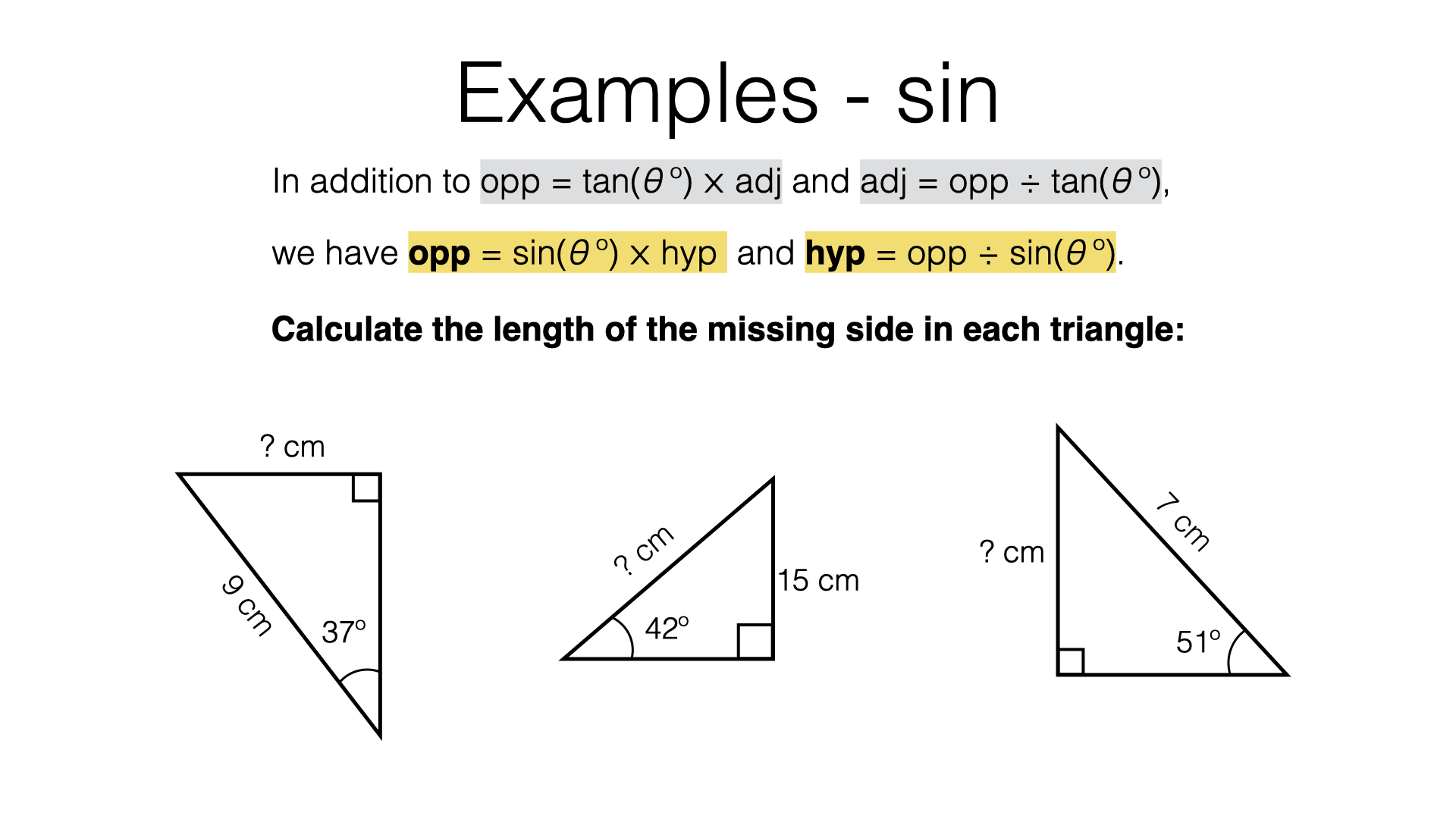
The inverse trigonometric functions (sin-1, cos-1, and tan-1) allow you to find the measure of an angle in a right triangle.All that you need to know are any two sides as well as how to use SOHCAHTOA.

To better understand certain problems involving aircraftand propulsionit is necessary to use some mathematical ideas fromtrigonometry,the study of triangles.Let us begin with some definitions and terminologywhich we will use on this slide.A right triangle is athree sided figure with one angle equal to 90 degrees. A 90 degree angle iscalled a right angle which gives the right triangle its name.We pick one of the two remaining angles and label it cand the third angle we label d.The sum of the angles of any triangle is equal to 180 degrees.If we know the value of c,we then know that the value of d:
- Cos hypotenuse q= hypotenuse sec adjacent q= opposite tan adjacent q= adjacent cot opposite q= Unit circle definition For this definition q is any angle. Sin 1 y qy 1 csc y q= cos 1 x qx 1 sec x q= tan y x q= cot x y q= Facts and Properties Domain The domain is all the values of q that can be plugged into the function. Sinq, q can be any.
- Sin Cos Tan Chart. Though we can find the values of cos, sin, and tan using the calculator, there is a chart with some standard angles 0 o, 30 o, 45 o, 60 o, and 90 o. Tips to remember sin cos tan table: The things that you need to memorize from this chart are: The angles 0 o, 30 o, 45 o, 60 o, and 90 o in order.
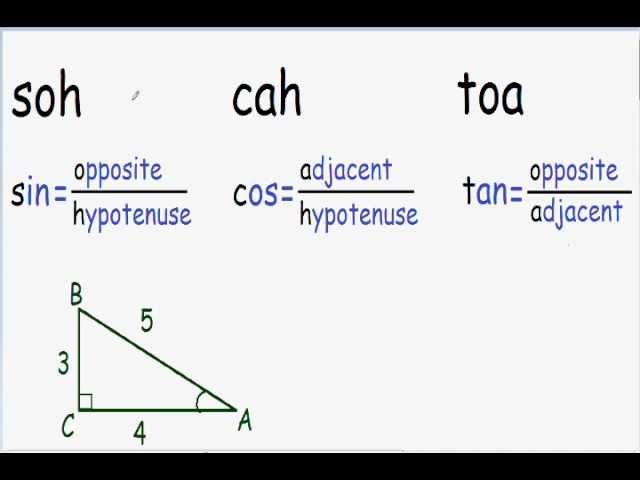
- Sin, cos and tan Before we can use trigonometric relationships we need to understand how to correctly label a right-angled triangle. There are three labels we will use: Hypotenuse - The longest.
90 + c + d = 180
d = 180 - 90 - c
d = 90 - c
We define the side of the triangle opposite from the right angle tobe the hypotenuse. It is the longest side of the three sidesof the right triangle. The word 'hypotenuse' comes from two Greek wordsmeaning 'to stretch', since this is the longest side.We label the hypotenuse with the symbol h.There is a side opposite the angle c which we label ofor 'opposite'. The remaining side we label a for 'adjacent'.The angle c is formed by the intersection of the hypotenuse hand the adjacent side a.
We are interested in the relations between the sides and the angles ofthe right triangle.Let us start with some definitions.We will call theratioof the opposite side of a right triangle to the hypotenusethe sine and give it the symbol sin.
sin = o / h
The ratio of the adjacent side of a right triangle to the hypotenuse is called thecosine and given the symbol cos.
cos = a / h
Finally, the ratio of the opposite side to the adjacent side is called thetangent and given the symbol tan.
tan = o / a
We claim that the value of each ratio depends only on the value ofthe angle c formed by the adjacent and the hypotenuse.To demonstrate this fact,let's study the three figures in the middle of the page.In this example, we havean 8 foot ladder that we are going to lean against a wall. The wall is8 feet high, and we have drawn white lines on the walland blue lines along the ground at one foot intervals.The length of the ladder is fixed.If we incline the ladder so that its base is 2 feet from the wall,the ladder forms an angle of nearly 75.5 degrees degrees with the ground.The ladder, ground, and wall form a right triangle. The ratio of the distance from thewall (a - adjacent), to the length of the ladder (h - hypotenuse), is 2/8 = .25.This is defined to be the cosine of c = 75.5 degrees. (Onanother pagewe will show that if the ladder was twice as long (16 feet),and inclined at the same angle(75.5 degrees), that it would sit twice asfar (4 feet) from the wall. The ratio stays the same for any right trianglewith a 75.5 degree angle.)If we measure the spot on the wall where the ladder touches (o - opposite), the distance is7.745 feet. You can check this distance by using thePythagorean Theoremthat relates the sides of a right triangle:
h^2 = a^2 + o^2
o^2 = h^2 - a^2
o^2 = 8^2 - 2^2
o^2 = 64 - 4 = 60
o = 7.745

The ratio of the opposite to the hypotenuse is .967 and defined to be thesine of the angle c = 75.5 degrees.
Now suppose we incline the 8 foot ladder so that its base is 4 feet from the wall.As shown on the figure, the ladder is now inclined at a lower angle than in thefirst example. The angle is 60 degrees, and the ratio of the adjacent tothe hypotenuse is now 4/8 = .5 . Decreasing the angle cincreases the cosine of the angle because the hypotenuse is fixedand the adjacent increases as the angle decreases. If we incline the 8 footladder so that its base is 6 feet from the wall, the angle decreases toabout 41.4 degrees and the ratio increases to 6/8, which is .75.As you can see, for every angle,there is a unique point on the ground that the 8 foot ladder touches,and it is the same point every time we set the ladder to that angle.Mathematicians call this situation afunction.The ratio of the adjacentside to the hypotenuse is a function of the angle c, so we can write thesymbol as cos(c) = value.
Notice also that as the cos(c) increases, the sin(c) decreases.If we incline the ladder so that the base is 6.938 feet from the wall,the angle c becomes 30 degrees and the ratio of the adjacent tothe hypotenuse is .866.Comparing this result with example two we find that:
cos(c = 60 degrees) = sin (c = 30 degrees)
sin(c = 60 degrees) = cos (c = 30 degrees)
We can generalize this relationship:

sin(c) = cos (90 - c)
90 - c is the magnitude of angle d. That is why wecall the ratio of the adjacent and the hypotenuse the 'co-sine' of the angle.
sin(c) = cos (d)
Since the sine, cosine, and tangent are all functions of the angle c, we candetermine (measure) the ratios once and produce tables of the values of thesine, cosine, and tangent for various values of c. Later, if we know thevalue of an angle in a right triangle, the tables will tell us the ratioof the sides of the triangle.If we know the length of any one side, we can solve for the length of the othersides.Or if we know the ratio of any two sides of a right triangle, we canfind the value of the angle between the sides.We can use the tables to solve problems.Some examples of problems involving triangles and angles include theforces on an aircraft in flight,the application oftorques,and the resolution of thecomponentsof a vector.
Here are tables of the sine, cosine, and tangent which you can use to solveproblems.
Activities:Guided Tours
Navigation ..
- Beginner's Guide Home Page
To better understand certain problems involving aircraftand propulsionit is necessary to use some mathematical ideas fromtrigonometry,the study of triangles.Let us begin with some definitions and terminologywhich we will use on this slide.A right triangle is athree sided figure with one angle equal to 90 degrees. A 90 degree angle iscalled a right angle which gives the right triangle its name.We pick one of the two remaining angles and label it cand the third angle we label d.The sum of the angles of any triangle is equal to 180 degrees.If we know the value of c,we then know that the value of d:
90 + c + d = 180
d = 180 - 90 - c
d = 90 - c
We define the side of the triangle opposite from the right angle tobe the hypotenuse. It is the longest side of the three sidesof the right triangle. The word 'hypotenuse' comes from two Greek wordsmeaning 'to stretch', since this is the longest side.We label the hypotenuse with the symbol h.There is a side opposite the angle c which we label ofor 'opposite'. The remaining side we label a for 'adjacent'.The angle c is formed by the intersection of the hypotenuse hand the adjacent side a.
We are interested in the relations between the sides and the angles ofthe right triangle.Let us start with some definitions.We will call theratioof the opposite side of a right triangle to the hypotenusethe sine and give it the symbol sin.
sin = o / h
The ratio of the adjacent side of a right triangle to the hypotenuse is called thecosine and given the symbol cos.
cos = a / h
Finally, the ratio of the opposite side to the adjacent side is called thetangent and given the symbol tan.
tan = o / a
We claim that the value of each ratio depends only on the value ofthe angle c formed by the adjacent and the hypotenuse.To demonstrate this fact,let's study the three figures in the middle of the page.In this example, we havean 8 foot ladder that we are going to lean against a wall. The wall is8 feet high, and we have drawn white lines on the walland blue lines along the ground at one foot intervals.The length of the ladder is fixed.If we incline the ladder so that its base is 2 feet from the wall,the ladder forms an angle of nearly 75.5 degrees degrees with the ground.The ladder, ground, and wall form a right triangle. The ratio of the distance from thewall (a - adjacent), to the length of the ladder (h - hypotenuse), is 2/8 = .25.This is defined to be the cosine of c = 75.5 degrees. (Onanother pagewe will show that if the ladder was twice as long (16 feet),and inclined at the same angle(75.5 degrees), that it would sit twice asfar (4 feet) from the wall. The ratio stays the same for any right trianglewith a 75.5 degree angle.)If we measure the spot on the wall where the ladder touches (o - opposite), the distance is7.745 feet. You can check this distance by using thePythagorean Theoremthat relates the sides of a right triangle:
h^2 = a^2 + o^2
o^2 = h^2 - a^2
o^2 = 8^2 - 2^2
o^2 = 64 - 4 = 60
o = 7.745
The ratio of the opposite to the hypotenuse is .967 and defined to be thesine of the angle c = 75.5 degrees.
Now suppose we incline the 8 foot ladder so that its base is 4 feet from the wall.As shown on the figure, the ladder is now inclined at a lower angle than in thefirst example. The angle is 60 degrees, and the ratio of the adjacent tothe hypotenuse is now 4/8 = .5 . Decreasing the angle cincreases the cosine of the angle because the hypotenuse is fixedand the adjacent increases as the angle decreases. If we incline the 8 footladder so that its base is 6 feet from the wall, the angle decreases toabout 41.4 degrees and the ratio increases to 6/8, which is .75.As you can see, for every angle,there is a unique point on the ground that the 8 foot ladder touches,and it is the same point every time we set the ladder to that angle.Mathematicians call this situation afunction.The ratio of the adjacentside to the hypotenuse is a function of the angle c, so we can write thesymbol as cos(c) = value.
Notice also that as the cos(c) increases, the sin(c) decreases.If we incline the ladder so that the base is 6.938 feet from the wall,the angle c becomes 30 degrees and the ratio of the adjacent tothe hypotenuse is .866.Comparing this result with example two we find that:
cos(c = 60 degrees) = sin (c = 30 degrees)
sin(c = 60 degrees) = cos (c = 30 degrees)
We can generalize this relationship:
sin(c) = cos (90 - c)
90 - c is the magnitude of angle d. That is why wecall the ratio of the adjacent and the hypotenuse the 'co-sine' of the angle.
sin(c) = cos (d)
Since the sine, cosine, and tangent are all functions of the angle c, we candetermine (measure) the ratios once and produce tables of the values of thesine, cosine, and tangent for various values of c. Later, if we know thevalue of an angle in a right triangle, the tables will tell us the ratioof the sides of the triangle.If we know the length of any one side, we can solve for the length of the othersides.Or if we know the ratio of any two sides of a right triangle, we canfind the value of the angle between the sides.We can use the tables to solve problems.Some examples of problems involving triangles and angles include theforces on an aircraft in flight,the application oftorques,and the resolution of thecomponentsof a vector.
Here are tables of the sine, cosine, and tangent which you can use to solveproblems.
Activities:Sin Tan Cos Calculator
Guided Tours
Navigation ..
Sin Cos Tan Def
- Beginner's Guide Home Page